| |
Random Walks
Let us start the discussion with a simple illustration and few practical examples.
Illustrative example for explaining the concept of random walk
Assume there is a particle which at time 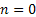 is at any particular position or state, say is at any particular position or state, say 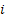 , i.e., , i.e., 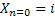 , and assume the movement of the particular is along the x-axis. This being the first simple example we will consider the movement is along one dimension only. Now suppose at time , and assume the movement of the particular is along the x-axis. This being the first simple example we will consider the movement is along one dimension only. Now suppose at time 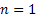 , we are in the , we are in the 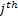 position or state , i.e., position or state , i.e., 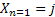 . Assume the movement that the particle has from the . Assume the movement that the particle has from the 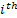 state to the state to the 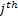 state in the time between state in the time between 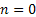 to to 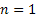 happened due to the fact that the particular had a jump or moved a step, which we denote by happened due to the fact that the particular had a jump or moved a step, which we denote by 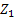 . Furthermore at . Furthermore at 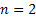 assume the particular undergoes another jump Z2, such that Z1 and Z2 are identically and independently distributed (i.i.d). For ease of explanation consider the diagrams below (Figure 1.12 and Figure 1.13) which is self explanatory. In the first figure (Figure 1.12) we see how the particle moves from the assume the particular undergoes another jump Z2, such that Z1 and Z2 are identically and independently distributed (i.i.d). For ease of explanation consider the diagrams below (Figure 1.12 and Figure 1.13) which is self explanatory. In the first figure (Figure 1.12) we see how the particle moves from the 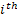 state (which is occupies at state (which is occupies at 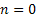 ) to subsequent states denoted by ) to subsequent states denoted by 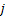 , , 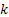 , , 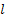 , , 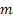 and so on at instances of time denoted by and so on at instances of time denoted by 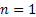 , , 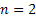 , , 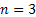 , , 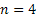 , etc. The colour schemes makes it clear how the movement of the particle takes place at each instance and these jumps or morevement are one step at a time. While on the other hand Figure 1.13 gives an arbitrary snapshot of the movement of the particle, and obviously there are other combinations of movements of the particle also. , etc. The colour schemes makes it clear how the movement of the particle takes place at each instance and these jumps or morevement are one step at a time. While on the other hand Figure 1.13 gives an arbitrary snapshot of the movement of the particle, and obviously there are other combinations of movements of the particle also.
|
Figure 1.12: Illustration of random walk |
|