Example 1.5
Let 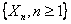 be a stochastic process with be a stochastic process with 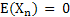 and and 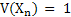 , , 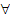 n and uncorrelated random variables (r.v's), then n and uncorrelated random variables (r.v's), then
Hence
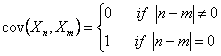 , which implies that it is covariance stationary , which implies that it is covariance stationary
Furthermore if the random variables (r.v's) are i.i.d, then the stochastic process is strictly stationary
Note : A stochastic process is not stationary in any sense is called evolutionary or non-stationary.
One should remember that modelling with continuous stochastic process is easier than working with stochastic processes which are not continuous, i.e., discrete. For example one may consider stock prices movement to be continuous. But in general the prices move in quantum of say 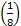 or or 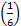 of a Re. 1. So in real sense the stock price movement is not continuous, even though for all practical purposes when trying to model stock prices or study them, we consider stock price movement as continuous. We will study stochastic processes which are called diffusion processes, the illustration of which is given below (Figure 1.11). of a Re. 1. So in real sense the stock price movement is not continuous, even though for all practical purposes when trying to model stock prices or study them, we consider stock price movement as continuous. We will study stochastic processes which are called diffusion processes, the illustration of which is given below (Figure 1.11).
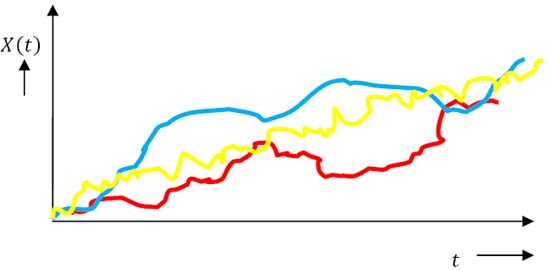 |
Figure 1.11: Diffusion process which may be used to define stock price movements |
|