One may add that the marginal distributions of 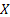 an an 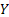 relative to their joint distributions are identical with the distributions of relative to their joint distributions are identical with the distributions of 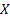 and and 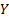 taken individually one at a time, i.e., taken individually one at a time, i.e.,
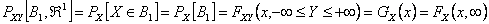
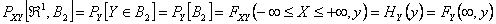
and 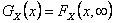 and and 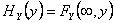 have the properties of the univariate distributions of X and Y respectively. have the properties of the univariate distributions of X and Y respectively.
In a similar way we can define the marginal distributions in the case when we have 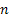 number of r.v., number of r.v., 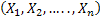 , such that each has the required probability space is , such that each has the required probability space is 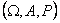 . Let us also define . Let us also define
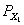 ,…, ,…, 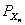 as the probability measure induced by as the probability measure induced by 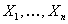 respectively on the space, defined as respectively on the space, defined as 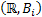 , where , where 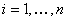 . If . If 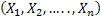 are r.v., such that they are defined on are r.v., such that they are defined on 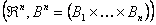 , where , where 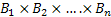 are arbitrary Borel sets identifined for are arbitrary Borel sets identifined for 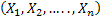 then then 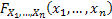 be the joint distribution function defined for the r.v., be the joint distribution function defined for the r.v., 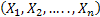 , where , where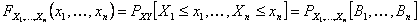 . Then . Then 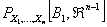 represents the probability that the variable represents the probability that the variable 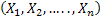 will take a value belonging to the area marked by will take a value belonging to the area marked by 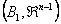 , i.e., the probability , i.e., the probability 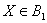 , irrespective of the value of , irrespective of the value of 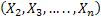 (remember (remember 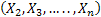 can take any value in the entire domain of can take any value in the entire domain of 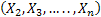 , i.e., , i.e., 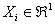 , where , where 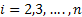 ). In a similar way we can define ). In a similar way we can define 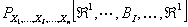 and one can write and one can write 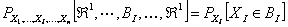 , , for some r.v., XI. , , for some r.v., XI.
Thus the probabilities 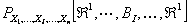 for varying values of XI defines the m arginal distribution of X1 relative to the joint distribution of for varying values of XI defines the m arginal distribution of X1 relative to the joint distribution of 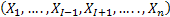 . In a very simple sense it means we project the mass of the joint distribution on the sub-space of the variable X1. In a similar sense we can also say that the marginal distributions of XI on . In a very simple sense it means we project the mass of the joint distribution on the sub-space of the variable X1. In a similar sense we can also say that the marginal distributions of XI on 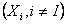 relative to their joint distribution is identical with the distribution of X1 taken individually one at a time, i.e., relative to their joint distribution is identical with the distribution of X1 taken individually one at a time, i.e.,
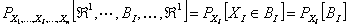
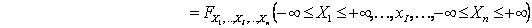

For a stochastic process we will consider the joint distribution, Thus given 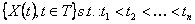 we are interested to find the joint distribution of we are interested to find the joint distribution of 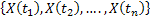 . .
Note
We say a stochastic process is a stationary joint distribution if it is invariant to the shift of time, i.e., if the joint distribution of 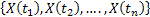 and and 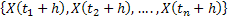 are the same are the same 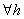 . This is usually called stationary of order n as we have n ordered time points. If a stochastic process is said is said to be of order n for every value of . This is usually called stationary of order n as we have n ordered time points. If a stochastic process is said is said to be of order n for every value of 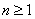 , then the stochastic process is called strictly stationary. , then the stochastic process is called strictly stationary. |