| |
Marginal Distributions
Let us again define two r.v., 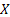 , , 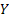 such that the required probability space is such that the required probability space is 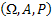 . Let us also define . Let us also define 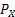 and and 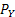 as the probability measure induced by as the probability measure induced by 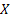 and and 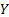 respectively on the space, defined by respectively on the space, defined by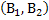 ..Now if ..Now if 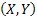 are r.vs, such that they are defined on are r.vs, such that they are defined on  , where , where 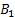 and and 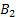 are arbitrary Borel sets defined for are arbitrary Borel sets defined for 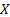 and and 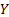 and and 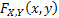 be the joint distribution function defined for the r.v., be the joint distribution function defined for the r.v., 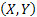 , where , where 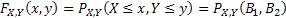 is true,then is true,then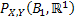 represents the probability that the variable represents the probability that the variable 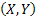 will take a value belonging to the area marked by will take a value belonging to the area marked by 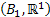 , i.e., the probability , i.e., the probability 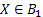 , irrespective of the value of , irrespective of the value of 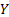 (remember (remember 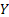 can take any value in the entire domain of Y, i.e., can take any value in the entire domain of Y, i.e., 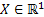 ). In a similar way we can define ). In a similar way we can define 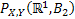 . We can write . We can write 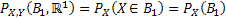 and and 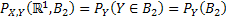 . .
Thus the probabilities 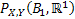 (Figure 1.9) for varying values of (Figure 1.9) for varying values of 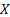 defines the marginal distribution of defines the marginal distribution of 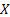 relative to the joint distribution of relative to the joint distribution of 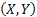 . In a very simple sense it means we project the mass of the joint distribution on the sub-space of the variable . In a very simple sense it means we project the mass of the joint distribution on the sub-space of the variable 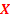 . Similarly we can define the probabilities . Similarly we can define the probabilities 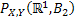 (Figure 1.10) for varying values of (Figure 1.10) for varying values of 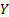 such that it defines the marginal distribution of such that it defines the marginal distribution of 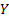 relative to the joint distribution of relative to the joint distribution of 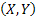 and it implies that we project the mass of the joint distribution on the sub-space of the variable and it implies that we project the mass of the joint distribution on the sub-space of the variable 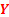 . .
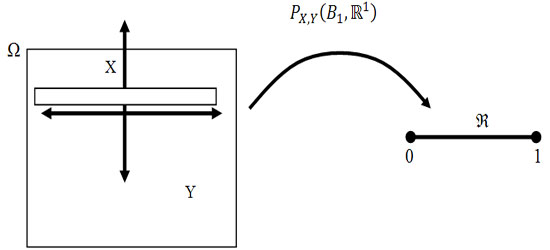 |
Figure 1.9: Illustration of 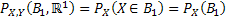 |
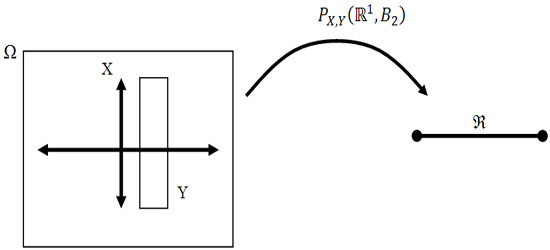 |
Figure 1.10: Illustration of 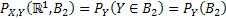
|
|