For the ease of understanding we have a look at the bivariate case mapping which is shown in Figure 1.8.

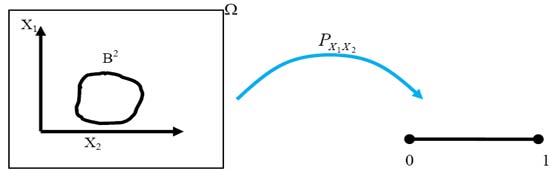Figure 1.8: Bivariate probability distribution functional mapping

If one considers the tossing of an unbiased coin then X(w) is either X(H) or X(T) and as per convention (nothing sacrosanct in the notation as such), we denote X(H) = 1 and X(T) = 0. Then what would be the value of P[X(H) = 1] or P[X(T) = 0] is what is the finally probability function (generally the distribution function denoted by cumulative distribution function) which is of interest to us for both theoretical as well as practical purposes. So for example (again the same example of tossing the unbiased die) we have 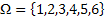, and we can have X(1) = X(2) = X(3) = 0 while X(4) = X(5) = (X(6) = 1. Later on we have the mapping, such that P[X(1)] = …. = P[X(6)] = 1/6. This simple concept can be extended for the higher dimension also and we can have the marginal, conditional as well as the joint distribution functions mapped as required.