| |
Moments
Few important moments which are of interest to us for any theoretical as well as empirical distributions are: mean, variance/standard deviation, covariance, skewnesss (3rd order moment), kurtosis (4th order moments) and other higher moments. Now if E[X(t)] is independent of t, then we know that E[X(t)] is a constant.
For moments we know the following
1st order moment is expected value or mean value or average value (we are being very generous in our terminology is trying to define the 1st moment, even though in the strict sense expected value, mean value, average value are slightly different concepts more pertaining to the property of the population and sample). The symbol of the 1st moment is E(X)
2nd order moment is used to find variance and the variance is given by E[{X – E(X)}2]. The concept of standard deviation, sample variance, standard error are also some metrics which can be calculated using the 2nd moment. 3rd order moments can be used to find skewness, and the general formulae is E[{X - E(X)}3]. 4th order moments can be used to find kurtosis and the general formulae is E[{X - E(X)}4]. rth order moment is denoted by E(Xr). rth order central moment is denoted by E[{X - E(X)}r]. In this case the central moment is calculated about the mean, E(X). In many cases we calculate the general moment called the raw moment and we have E{X - a}r which is the moment of order 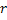 , where this , where this 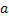 can be any point. can be any point.
Similarly for a stochastic process we can find the expected value, variance as well as the higher moments.Now the variance is given by
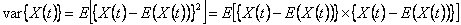 , while covariance is given as , while covariance is given as 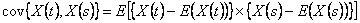 . .
Note
| 1. If we take E[X(t)] as constant, then we have |
| |
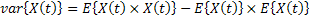 |
| |
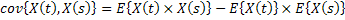 |
| 2. If we take E[X(t)] as zero, then we have |
| |
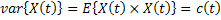 , where , where 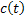 is a constant is a constant |
| |
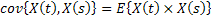 = =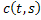 , where , where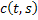 is a constant is a constant |
3. If 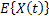 and and 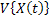 does not depend on t, then cov{X(t),X(s)} only depends on does not depend on t, then cov{X(t),X(s)} only depends on 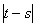 and is called covariance stationary or weekly stationary or stationary and in the wide sense stationary. We will discuss about these later on. and is called covariance stationary or weekly stationary or stationary and in the wide sense stationary. We will discuss about these later on. |
|