Section II: Swing Equation
Let us consider a three-phase synchronous alternator that is driven by a prime mover. The equation of motion of the machine rotor is given by

|
(9.6) |
where
| J |
is the total moment of inertia of the rotor mass in kgm2 |
Tm
|
is the mechanical torque supplied by the prime mover in N-m |
| Te |
is the electrical torque output of the alternator in N-m |
| θ |
is the angular position of the rotor in rad |
Neglecting the losses, the difference between the mechanical and electrical torque gives the net accelerating torque Ta . In the steady state, the electrical torque is equal to the mechanical torque, and hence the accelerating power will be zero. During this period the rotor will move at synchronous speed ωs in rad/s.
The angular position θ is measured with a stationary reference frame. To represent it with respect to the synchronously rotating frame, we define

|
(9.7) |
where δ is the angular position in rad with respect to the synchronously rotating reference frame. Taking the time derivative of the above equation we get
 |
(9.8) |
Defining the angular speed of the rotor as
we can write (9.8) as
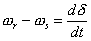
|
(9.9) |
We can therefore conclude that the rotor angular speed is equal to the synchronous speed only when dδ / dt is equal to zero. We can therefore term dδ / dt as the error in speed. Taking derivative of (9.8), we can then rewrite (9.6) as
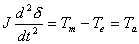
|
(9.10) |
Multiplying both side of (9.11) by ωm we get

|
(9.11) |
where Pm , Pe and Pa respectively are the mechanical, electrical and accelerating power in MW.
We now define a normalized inertia constant as

|
(9.12) |
Substituting (9.12) in (9.10) we get

|
(9.13) |
In steady state, the machine angular speed is equal to the synchronous speed and hence we can replace ωr in the above equation by ωs. Note that in (9.13) Pm , Pe and Pa are given in MW. Therefore dividing them by the generator MVA rating Srated we can get these quantities in per unit. Hence dividing both sides of (9.13) by Srated we get
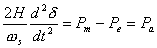 per unit per unit
|
(9.14) |
Equation (7.14) describes the behaviour of the rotor dynamics and hence is known as the swing equation. The angle δ is the angle of the internal emf of the generator and it dictates the amount of power that can be transferred. This angle is therefore called the load angle .
Example 9.2 |