Economic Sharing of Loads between Different Plants

So far we have considered the economic operation of a single plant in which we have discussed how a particular amount of load is shared between the different units of a plant. In this problem we did not have to consider the transmission line losses and assumed that the losses were a part of the load supplied. However if now consider how a load is distributed between the different plants that are joined by transmission lines, then the line losses have to be explicitly included in the economic dispatch problem. In this section we shall discuss this problem.

When the transmission losses are included in the economic dispatch problem, we can modify (5.4) as

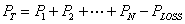(5.11)

where P_LOSS is the total line loss. Since P_T is assumed to be constant, we have

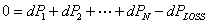(5.12)

In the above equation dP_LOSS includes the power loss due to every generator, i.e.,

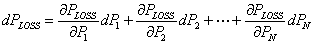(5.13)

Also minimum generation cost implies df_T = 0 as given in (5.5). Multiplying both (5.12) and (5.13) by λ and combining we get

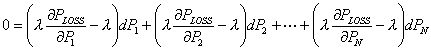(5.14)

Adding (5.14) with (5.5) we obtain

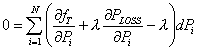(5.15)

The above equation satisfies when

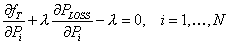(5.16)

Again since

from (5.16) we get

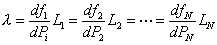(5.17)

where L_i is called the penalty factor of load- i and is given by

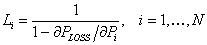(5.18)

Example 5.4

Consider an area with N number of units. The power generated are defined by the vector

Then the transmission losses are expressed in general as

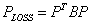(5.19)

where B is a symmetric matrix given by

The elements B_ij of the matrix B are called the loss coefficients . These coefficients are not constant but vary with plant loading. However for the simplified calculation of the penalty factor L_i these coefficients are often assumed to be constant.

When the incremental cost equations are linear, we can use analytical equations to find out the economic settings. However in practice, the incremental costs are given by nonlinear equations that may even contain nonlinearities. In that case iterative solutions are required to find the optimal generator settings.