The Entropy model of trip distribution, unlike the previous models discussed here, is not a behavioral model. That is, the entropy model does not strive to predict the trip distribution by modeling the human behavioral aspects related to choosing a destination. This model, on the other hand, attempts to determine a distribution of trips which is most likely to occur assuming that each trip occurs independently of another.
For a total number of ![]() trips in a network, it is assumed that there are a
total of
trips in a network, it is assumed that there are a
total of ![]() independent decisions. Obviously, a given trip distribution
matrix can be obtained through different combination of the decisions.
Specifically, the number of ways a trip distribution matrix [
independent decisions. Obviously, a given trip distribution
matrix can be obtained through different combination of the decisions.
Specifically, the number of ways a trip distribution matrix [![]() ],
can be obtained is:
],
can be obtained is:
| (23) |
| (24) |
| (25) |
| (26) |
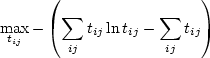 , this is equivalent to solving
, this is equivalent to solving
The unconstrained optimization problem in Equation ![]() is the standard
maximum entropy model of trip distribution. However, one can
easily incorporate various constraints in this model. Some of the constraints
which are often included in the maximum entropy model are
is the standard
maximum entropy model of trip distribution. However, one can
easily incorporate various constraints in this model. Some of the constraints
which are often included in the maximum entropy model are
![]() ,
,
![]() ,
,
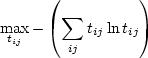 observed average trip length, etc.
observed average trip length, etc.
Discussion: The constraints can easily be
incorporated in the function to be maximized by constructing a Lagrangian.
The Lagrangian can then be differentiated with respect to the ![]() 's and
and the Lagrange multipliers to obtain a set of expressions which can
be equated to zero. These equations when solved will give the estimate of the
trip distribution.
's and
and the Lagrange multipliers to obtain a set of expressions which can
be equated to zero. These equations when solved will give the estimate of the
trip distribution.
Also note that this method does not use any calibration constants and hence the issue of calibrating the model does not arise.