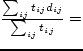 ,
, Modal split models aim to determine the number of trips on different modes given the travel demand between different pairs of nodes (zones). These models try to mathematically describe the mode choice phase of the sequential demand analysis procedure. Generally choice models are used for modal split analysis. That is, it is assumed that the probability of choosing a particular mode is the probability that the perceived utility from that mode is greater than the perceived utility from each of the other available modes. Since, choice models were discussed while presenting destination choice models in the section on trip distribution they are not repeated here. This section only discusses the factors which are generally assumed to affect the perceived utility of modes. An example problem is also solved.
The factors which affect the choice of a mode (and hence the perceived utility from a mode) are:
Example
For a particular zone pair, three modes of travel between the zones
exist -- private transport like
automobiles (PT), bus (B), and urban rapid transit system like
local trains (RT). It is given that all trip makers have access to private
transport and that the perceived utility of a mode, 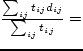 ,
, ![]() is given by
is given by
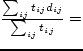 ,
, 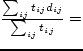 ,
, 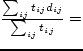 , and
, and
| Mode | Variable values | |||
| PT | 65 | 60 | 0 | 1 |
| B | 75 | 5 | 5 | 0 |
| RT | 25 | 8 | 20 | 0 |
Solution
First, calculate the perceived utility for each mode:
Next, use Logit model to determine the probability, ![]() that a
particular mode,
that a
particular mode, 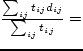 , will be chosen.
, will be chosen.
Hence, 302 trips will be made using private transport, 324 will use buses, and 374 will use the rapid transit system.