Intervening opportunities model

The postulate of travel behaviour on which this model is based, from Stouffer [#!sto1!#], is that the probability of choice of a particular destination (from a given origin for a particular trip purpose) is proportional to the opportunities for trip purpose satisfaction at the destination and inversely proportional to all such opportunities that are closer to the origin. The inverse proportionality to closer opportunities can be interpreted as proportionality to the probability that none of the closer destinations (opportunities) are chosen. Thus, in this model, the in-situ attractive properties of the destination are modeled as opportunities and the impedances are measured in terms of the number of opportunities which are closer.

In order to formulate the postulate as a mathematical model, the following notation are used:

$L$ : 		 Constant of proportionality (or calibration constant). 

$J$ : 		 Total number of destinations. 

$j$ : 		 Index indicating the position of a destination (from the givenorigin); 

$j=1$ for the nearest destination and $j=J$ for the farthest. 

$V_i(j)$ : 		 Cumulative function of opportunities up to andincluding the $j^{th}$ destination 


from origin $i$. 

$P_i(j)$ : 		 Probability a destination is chosen from the $i^{th}$origin by the time the $j^{th}$ 


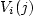
destination is reached.

$\pi_{ij}$ : 		 Probability that the $j^{th}$ destination is chosen fromthe $i^{th}$ origin.

Based on the postulate the following expression can be written:

$$dP_i(j) = L \{1-P_i(j)\} dV_i(j)$$ (11)

This expression states that a little addition in opportunities ($dV_i(j)$) after the $j^{th}$ destination causes a small increase in the probability ($dP_i(j)$). This increase is proportional to the probability that no destination is chosen by the $j^{th}$ destination and the amount of additional opportunities.

Using $P_i(0)=0$ (since it is assumed that $V_i(0) = 0$ ) and solving the differential equation one gets

$$P_i(j) = 1 - e^{-LV_i(j)}$$ (12)

and since, by definition, $\pi_{ij} = P_i(j) - P_i(j-1)$

$$\pi_{ij} = e^{-LV_i(j-1)} - e^{-LV_i(j)}$$ (13)

Notice, however, nothing guarantees that $\sum_j \pi_{ij} = 1$. In fact, $1 -\sum_j \pi_{ij}$ could be interpreted as the probability that no destination is chosen. This, however, poses a problem in the sequential demand analysis framework because if no destination is chosen then it leads to a situation where a trip is produced but does not go anywhere. In order to correct this anomaly, the $\pi_{ij}$ obtained in Equation  is modified by adding a constraint which states that a destination must be chosen from the set of available destinations thereby precluding the possibility of not choosing any destination. Mathematically this can be done in one of two ways, both leading to the same result. One could use Bayes theorem and determine the probability that destination $j$ is chosen given that a destination is chosen or one could simply normalize the $\pi_{ij}$'s obtained in Equation  by dividing the individual $\pi_{ij}$'s with $\sum_j \pi_{ij}$. In either case the modified $\pi_{ij}$, written as $\pi_{ij}^m$, is given by,

$$\pi_{ij}^m = \frac{e^{-LV_i(j-1)} - e^{-LV_i(j)}}{1-e^{-LV_i(J)}}$$ (14)

Note that the denominator can be looked upon as either (i) the probability a destination is chosen, $P(J)$ or (ii) $\sum_j \pi_{ij}$. (The reader should verify these claims).

Once the $\pi_{ij}^m$ are obtained the trips between $i$ and $j$ can be obtained as:

$$t_{ij} = \pi_{ij}^m T_i$$ (15)

Example

For the 1200 shopping trips from Zone A, three destinations exist. The destinations are Zones X, Y, and Z. The shopping areas available in each of the zones and their distances from Zone A are given in Table . Assuming a proportionality constant of 0.35 and assuming a thousand square meter of shopping area as one opportunity determine the trip distribution from Zone A.

表: Data for the example problem on intervening opportunities model

Zone	Shopping area	Distance from Zone A
	(in '000 sq.m.)	(in km)
X	2.0	7.0
Y	4.0	12.0
Z	2.0	4.0

Solution

First, the destinations should be arranged from the closest to the farthest; in this case, $j=1$ for Zone Z, $j=2$ for Zone X, and $j=3$ for Zone Y. Since there are only 3 destinations, $J=3$.

Next, $V_i(j)$ need to be determined; $V_A(1) = 2$, $V_A(2) = 4$, and $V_A(3) = 8$.

Using Equation  the $\pi_{AX}^m$, $\pi_{AY}^m$, and $\pi_{AZ}^m$ are calculated as follows:

$$\begin{eqnarray*} \pi_{AZ}^m = \pi_{A1}^m & = & \frac{1-e^{-2 \times 0.35}}{1-e^... ...times 0.35}-e^{-8 \times 0.35}}{1-e^{-8 \times 0.35}} = 0.198\\ \end{eqnarray*}$$

Therefore, the trip distribution from Zone A is given by

$$\begin{eqnarray*} t_{AX} = 0.266 \times 1200 & = & 319\\ t_{AY} = 0.198 \times 1200 & = & 238 \\ t_{AZ} = 0.536 \times 1200 & = & 643 \\ \end{eqnarray*}$$

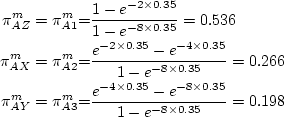
Discussion: Since the model gives the probability of choosing a destination from a given origin one may employ the maximum likelihood technique to calibrate the constant $L$. The likelihood function is similar to that given in Equation . However, it is seen that assumption of a constant $L$ is not very good for most problems. A varying $L$ adds complexity to the model and its calibration. For a more detailed discussion on intervening opportunity models one may see Kanafani [#!kan1!#] or Stouffer [#!sto1!#] or Ruiter [#!rui1!#].