The Gravity model uses the following basic form to determine the trips between
an origin zone ![]() and a destination zone
and a destination zone ![]() .
.
The expression
![]() may be thought of as a factor
which distributes the total trips produced by a zone among all the possible
destination zones. In this sense, the sum of the expression over all
destinations should be equal to unity.
may be thought of as a factor
which distributes the total trips produced by a zone among all the possible
destination zones. In this sense, the sum of the expression over all
destinations should be equal to unity.
Sometimes, in the gravity model, the number of trips
attracted to a zone (when such data is independently available), ![]() , is
used as a surrogate for
, is
used as a surrogate for ![]() . When such a
substitution is done the gravity model is typically written as
. When such a
substitution is done the gravity model is typically written as
Very often, in this case the following two constraints are imposed on the
gravity model to obtain the two calibration constants![]() :
:
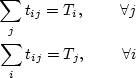 are
obtained as:
are
obtained as:
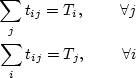 and vice versa.
and vice versa.
Example
Consider the following six zone model of a town. Zones 1, 2, and 3
are fully residential areas and Zones 4, 5 and 6 are purely shopping areas. The
shopping areas, shopping trips attracted (per day), shopping trips produced
(per day) and travel distances are as shown in Table ![]() . The
cells which have a ``-'' imply that those data are irrelevant to the problem.
Determine the trip
distribution between the zones for the following different scenarios:
. The
cells which have a ``-'' imply that those data are irrelevant to the problem.
Determine the trip
distribution between the zones for the following different scenarios:
(a) Use the origin constrained gravity model, assuming ![]() to be a linear
function of the shopping area (in square meters) with a slope of 0.01 and
constant term of 10. Also assume
to be a linear
function of the shopping area (in square meters) with a slope of 0.01 and
constant term of 10. Also assume 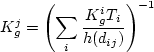 to be
to be ![]() where
where ![]() is the distance in kms.
is the distance in kms.
(b) Use the origin-destination constrained gravity model with relevant
assumptions same as those in (a).
Solution
Part a
The trips of interest here are ![]() , where
, where ![]() and
and
![]() . Also note, as per the problem description
. Also note, as per the problem description
![]() , and
, and
![]() . The trips
are given by Equation
. The trips
are given by Equation ![]() .
.
Part b
In this case, the only difference from Part (a) is that the trips are given by
Equation ![]() and the constants of Equation
and the constants of Equation ![]() are given
in Equations
are given
in Equations ![]() and
and ![]() . The initial value of
. The initial value of ![]() is assumed to be the square root of the corresponding values obtained in the
previous part. These values of
is assumed to be the square root of the corresponding values obtained in the
previous part. These values of ![]() are used in Equation
are used in Equation ![]() to
obtain a set of
to
obtain a set of 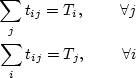 values which are in turn used in
Equation
values which are in turn used in
Equation ![]() to obtain a new set of
to obtain a new set of ![]() values. The process
continues till all the
values. The process
continues till all the ![]() and
and 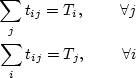 values converge. The final values
of
values converge. The final values
of ![]() and
and 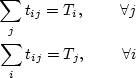 obtained are as follows:
obtained are as follows:
Final values of ![]()
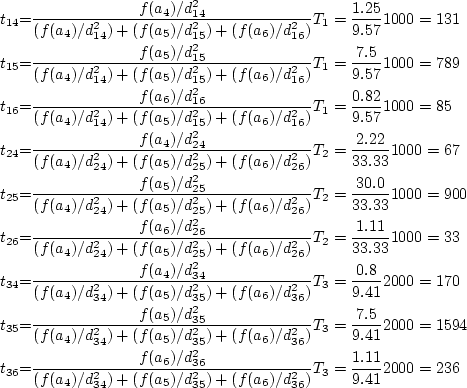 ,
, ![]() , and
, and ![]()
Final values of 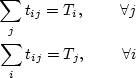
![]() ,
, ![]() , and
, and ![]()
Using these values of ![]() and
and 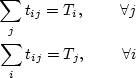 in Equation
in Equation ![]() the following
the following ![]() values are obtained:
values are obtained:
![]() ,
, ![]() , and
, and ![]()
![]() ,
, ![]() , and
, and ![]()
![]() ,
, ![]() , and
, and ![]()
The reader must verify that for the above trips
![]() and
and
![]() .
.
Discussion: It may be pointed out here that the
expression
![]() in
Equation
in
Equation ![]() may be viewed as
may be viewed as ![]() , the probability that
destination
, the probability that
destination ![]() is chosen from origin
is chosen from origin ![]() . Once such a view is taken, then the
Maximum likelihood technique
. Once such a view is taken, then the
Maximum likelihood technique ![]() can be used to
estimate the parameters of the gravity model. If observations on the trip
distribution between different origin-destination pairs are made and denoted
as
can be used to
estimate the parameters of the gravity model. If observations on the trip
distribution between different origin-destination pairs are made and denoted
as ![]() then the likelihood function can be written as
then the likelihood function can be written as