Design approach
As mentioned earlier, generally, the composite pavement is designed as overlay. The conventional overlay design applicable to composite pavement by (i) empirical and (ii) mechanistic approach and (iii) a special type of composite pavement as thin concrete pavement over bituminous pavement (known as ultra-thin white topping ) are discussed in the following:
Overlay design by empirical approach
The pavement thickness, as new pavement design, required to extend pavement life by a given overlay design period is estimated by using deflection, estimated strain, or some serviceability criteria; and the existing thickness is discounted to a some lower value than the original by using suitable factor(s). This may be called as the effective thickness of the existing pavement. The difference (i.e. the thickness deficiency ) between these two determines the overlay thickness. Thus,
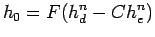 |
(36) |
where, h0 = the overlay thickness (either concrete or bituminous), F = empirical conversion factor for converting bituminous thickness to concrete thickness, or, vice versa, as applicable, hd = estimated overlay thickness (either concrete or bituminous), C = factor to convert the existing pavement thickness to equivalent effective pavement thickness (either concrete or bituminous), n is a factor which takes care of the bonding condition of the overlay. These factors are estimated from traffic data, or, by performing non-destructive testing (NDT), or, are derived from experience. The recommendations in Asphalt Institute (1983), AASHTO (1993), FAA (2006) etc., for estimating the bituminous overlay thickness over existing concrete pavement, are variants of this principle.
Overlay design by mechanistic approach
As per this approach, the composite pavement with some assumed overlay thickness is analysed mechanistically (as explained in the formulation). The critical stress-strain parameters at the critical locations are obtained, and the overlay thickness is adjusted so that the values are less than or equal to the allowable. For performing this exercise, the engineering parameters of the existing pavement layers (thickness, modulus, Poisson's ratio) needs to be known, and can be obtained through non-destructive testing. The engineering properties of the proposed overlay (modulus, Poisson's ratio) can be obtained from laboratory study.
Some guidelines (FAA 2006, NCHRP 2005) recommend similar procedure for estimating the concrete overlay thickness over existing bituminous pavement. As a simplified approach, it is suggested that, the whole bituminous pavement can be idealized as spring foundation, and the effective modulus of subgrade reaction can be obtained from field study.
Ultra-thin white topping
High strength concrete mixed with fibers are
generally used as ultra-thin rigid overlay over existing bituminous pavement
and is known as ultra-thin white-topping (UTW). The UTW pavement system is
analysed as a three-layer model (UTW layer, bituminous layer and a base layer
with equivalent modulus) assuming a degree of bonding between the pavement
layers (Murison and Smith 2002). Bonding in UTW makes the two layers (UTW
and bituminous layer) behave as a monolithic unit and share the load. The
neutral axis in concrete shifts from the middle of concrete layer towards
its bottom (refer Figure-30). Due to this shifting of neutral axis, the following
situations develop:
- Stress at the bottom of concrete layer reduces. Thus, the concrete layer can be made significantly thinner for the same loading as compared to a conventional white-topping overlay which generally has no or partial bond to the underlying bituminous layer (Goel and Das 2004).
- This however increases the corner stress at the top of the concrete layer. This may result in a possibility that the corner stress becomes critical than edge stress. In such a situation, the corner stress can be reduced by providing adequately thick bituminous layer as support to the UTW layer (Murison and Smith 2002).
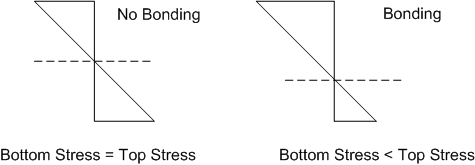
Figure 30: Stress distribution in bonded and unbonded layers (Goel and
Das 2004)
|