Module III : Few other topics on concrete pavement
Lecture 4: Composite Pavements
 

General formulation for composite pavement

Since the composite pavement is a combination of bituminous, granular, concrete, and subgrade layer, one needs to combine the individual models (Ioannides and Khazanovich 1998) of these layers to develop a formulation for composite pavement. Such an analysis problem will require (i) strain-displacement relationship, (ii) constitutive law, (iii) equilibrium equation and suitable (iv) boundary conditions.

Individual layers

From mechanics point of view, a composite pavement can be thought to be composed of three basic types of layers (Ioannides and Khazanovich 1998) viz. Burmister layer, subgrade layer and concrete layer . For simplicity in modeling the individual layers can be considered to be made up of homogenous, isotropic and elastic material. The basic characteristics of these layers can be mentioned as follows:

Burmister layer

The granular layer and the bituminous layer can be modelled as Burmister layer. A Burmister layer transfers the load through grain-to-grain interaction and it does not have flexural rigidity (Verstraeten 1967). It is assumed that this layer is infinite along the x and y direction and single circular loading may be considered as axi-symmetric about z axis.

Subgrade layer

The subgrade can be assumed as Boussinesq half-space which is infinite along x and y direction and semi-infinite along z (depth) direction (Jumikis 1969). The subgrade may also be modelled as elastic spring, for example, as Winkler spring bed, Pasternak foundation, Kerr foundation etc. and accordingly the different solutions can be obtained.



Concrete layer

The load in applied to concrete slab is resisted by bending action. The theory of plate bending is generally used in the analysis. If it is assumed that there is no deformation along the thickness of plate, then,σz = 0 at any point across the depth. The basic assumption of thin plate (known as Kirchhoff plate ) bending theory is that the thickness of the plate (h) is small as compared to the other dimensions and thus the effect of $ \tau_{xz}$ and $ \tau_{yz}$ on bending is negligible. For detailed discussion on formulation of rigid pavement, the lecture on analysis of concrete pavement may be referred.


Boundary conditions

Composite pavement is made up of a combination of these layers. Thus, having developed the governing equations of the individual layers, the analysis can be performed by using suitable boundary conditions. The boundary conditions for various interfaces may be mentioned as follows (Ioannides and Khazanovich 1998):

(1) At interface between two Burmister layers

$ \sigma_z^{i,b}=\sigma_z^{i+1,t}$  and $ \omega^{i,b}=\omega^{i+1,t}$ (for rough or smooth interface)
$ \tau_{rz}^{i,b}=\tau_{rz}^{i+1,t}$ and $ u^{i,b}=u^{i+1,t}$ (for rough interface) ; $ \tau_{rz}^{i,b}=0$ and $ \tau_{rz}^{i+1,t}=0$  (for smooth interface)

The superscript t indicates top and b indicates bottom of the interface. The superscript i indicates the ith layer. u  indicates the horizontal displacement and $ \omega$ indicates the vertical displacement.

(2) At interface between Burmister layer and rigid base

$ \omega^{n,b}=0$ (for rough or smooth surface)
$ u^{n,b}=0$ (for rough interface) and $ \tau_{rz}^{n,b}=0$ (for smooth interface)

(3) For Boussinesq half space

$ \omega=u=0$ at $ z=\infty$ and also, $ \sigma_z=\sigma_r=0$ at $ z=\infty$


(4) At interface between Burmister layer and cement concrete slab

$ \tau_{rz}^{n,b}=0$ and $ \omega^{n,b}=\omega^P$ where, $ \omega^P$ is the vertical deflection of the plate.

 

(5) At interface between Burmister layer and spring bed

$ \tau_{rz}^{n,b}=0$   and  $ \sigma_z^{n,b}=\sigma^S$, where $ \sigma^S$ is the vertical stress of the spring.

(6) At interface between two plates

$ q^{\star,i}=\sigma_z^{i,t}-\sigma_z^{i,b}$ ; provided $ i^{th}$ layer is not surface layer.
$ \omega^{i,t}=\omega^{i,b}=\omega^{i+1,t}=\omega^{i+1,b}=\omega^P$ (for pure bending), where, $ q^{\star}$ is the net vertical pressure.

(7) At the surface

When top surface is Busmister layer,
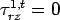
$ \sigma_z^{1,t}=-p$,   if   $ -a \le r \le a$;   otherwise   $ \sigma_z^{1,t}=0$,   p  is the pressure applied on circular area Also, $ \tau_{rz}^{1,t}=0$
When top surface is cement concrete slab,
$ \nabla^4 \omega^1=-p+\sigma_z^{2,t}$,  if   $ x^2+y^2 \le a^2$, otherwise, $ \nabla^4 \omega^1=0$

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
1
2