where K(θ) is the functional form of hydraulic conductivity. Therefore, the nature of the soil amount of soil water content influence the hydraulic conductivity in unsaturated soils. As the water content is reduced in the initially saturated soil, the air enters through a largest pore of the soil matrix. Hence, the effective flow channels are reduced which causes the reduction in unsaturated hydraulic conductivity as depicted in Fig. 3.14. Since the contribution to conductivity per unit cross-sectional area depends on the square of the pore radius, conductivity decreases much more rapidly than the amount of water in the soil, indicating a sudden drop in the conductivity in Fig. 3.14 after the air-entry value. Moreover, the contribution of larger pores having a radius, r, is better than the combination of smaller pores equal to the same radius as the viscosity effect is large. Therefore, as the larger pores get emptied first, the conductivity decreases exponentially. Further, reduction in water causes discontinuity of the flow paths in the nearly dry soil where the water is present in the form of occluded bubbles. Therefore, the conductivity is close to zero at this water content as shown in the figure. The Fig. 3.14 represents the general characteristic curve for K -function.

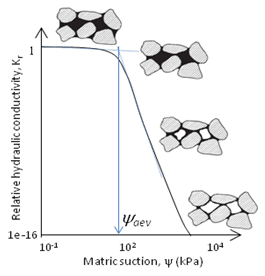
Fig. 3.14. Generalized hydraulic conductivity function

Several models representing the soil water retention and hydraulic conductivity have been used for smooth and continuous representation of the matric suction and hydraulic conductivity. Some of the important measurement techniques for hydraulic data and models are described in the following lectures.