The flow of water in a saturated soil was studied by applying Darcy's law in the basic soil mechanics text books. However, the question is: whether the Darcy's law is applicable for studying the flow through unsaturated soils. This question will be addressed here.

As we have seen in the previous lectures that a given soil may be unsaturated in several ways. The natural soil may contain two or more different liquids and air or only liquid and air. The saturation in such soils can be defined with respect to one of the fluids. The soils in nature, generally, contain air and water that are occupied in the pore space of the soil matrix. Therefore, the saturation here is in terms of the available water in the pore matrix. In such soils the air phase and water phase may form continuous phase or be separated by the other phases or soil particles. For the time being we assume that the soil only contains air and water in its pore space.

The fundamental dependent state variable responsible for the water flow through unsaturated soils is total suction, Ψ , or total suction head, h_t (or H ). The total driving head can be expressed as:

where h_g is the gravitational head, h m is the matric suction head, and h_o is the osmotic suction head. For most seepage problems, the osmotic suction head is neglected. This total suction head should be used in the Darcy's equation under unsaturated condition.

According to soil physics, the discharge velocity of water is understood to be proportional to the viscosity and density of the permeating fluid through the soil pores. The discharge velocity is high for permeating fluids having higher density and low viscosity vice versa. Further, the experimental observations, supported by the theoretical analysis, reveal that the discharge velocity is dependent on the pore size and pore size distribution. Therefore, the discharge velocity is

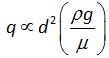..............................................................................................(3.5)

where d is the pore diameter (m), ρ the density of the fluid (kg/m³ ), m the dynamic viscosity of the fluid (N.s/m² ).

Combining the Darcy's observation on the dependency of discharge velocity on the hydraulic gradient, the above expression can be written as