Mean and the variance of the Gumbel distribution

The moment generating function for the Gumbel distribution is as follows;

The mean and the variance of the X_max are given below;

The mean, μ, equals to b + n_ea, where n_e is the Euler constant which is approximately equals to 0.5772.

The variance, σ² equals to

If any random variable X follows Weibull distribution then the log X follows type 1 extreme value distribution known as the Gumbel distribution.

Properties of the Gumbel Distribution

1. The mode of this distribution is b
2. If X is Gumbel distributed with parameters (b, a) and l, and m>0 are scalar constants, mX+l is Gumbel distributed with parameters (m*b+ l, )
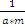3. If X₁, X₂ are two independent variables following Gumbel distribution with parameters (b₁, a) and (b₂, a), respectively, then the difference of these two variables, X^*, follow Logistic distribution.
   
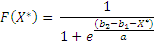
4. If X₁, X₂ are two independent variables following Gumbel distribution with parameters (b₁, a) and (b₂, a), respectively, then the maximum of these two variables follows Gumbel distribution with the following parameters
   
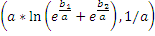
5. If X₁, X₂, …, X_n are independent variables following Gumbel distribution with parameters (b₁, a) and (b₂, a), …. (b_n, a),  respectively, then the maximum of these variables follows Gumbel distribution with the following parameters
   

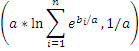
These Properties are useful when dealing with the choice related data where the error/unobserved components are considered to follow the Gumbel distribution.