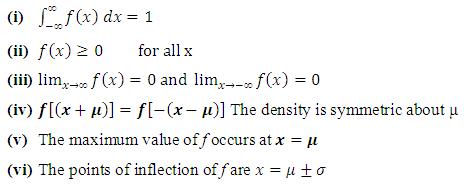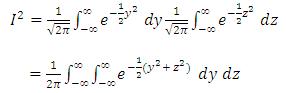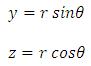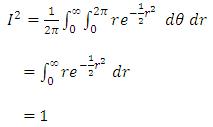Properties of the Normal Distribution
Following are the important properties of the Normal Distribution:
Proof for property (i):
A random variable X is said to have a normal distribution with mean μ ( -∞ < μ< ∞ ) and variance σ2 (σ2 > 0) if it has the density function:
Integrating and replacing with y:
Defining a second normally distributed variable, Z
Changing to polar coordinates with:
The integral becomes:
As I 2=1,I=1 since f must be positive everywhere.