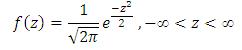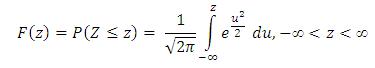Central limit theorem
If a random variable Y is the sum of n independent random variables that satisfy the following general conditions, for sufficiently large n, the variable Y is approximately normally distributed.
General conditions
- The individual normal random variable, Xi , contribute a negligible amount to the variance of the sum of all the n random variables
- It is also unlikely that a single random variable contributing significantly to the sum
If X1 , X2 , X3 , …., Xn are the set of n independent random variables with ith random variable having mean μi and variance σ2i , the resulting variable from the summation of all the n random variables is approximately normally distributed with mean and standard deviation
.
The following standardized variable,
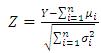
A linear transformation, Y = a + bX, of a random variable X with mean μ and variance σ2 results in a normal variable Y with mean a+bμ and the variance b2σ2 .
The Normal distribution
The most important distribution of a continuous random variable is the normal distribution. This has got several applications in Civil engineering. One of the illustrative applications in traffic engineering is with the distribution of the speed data. This distribution and its properties are very useful in dealing with the samples. It can also be used for approximating the other types of the probability distributions.
A continuous random variable X is said to follow the normal distribution if its pdf is
The cumulative distribution function for the normal variable is given below;
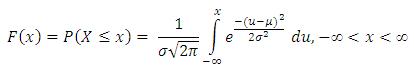
It is difficult to evaluate the above integral hence the random variable is transformed into a standard normal variable and the resulting CDF is used in obtaining the corresponding probabilities. The transformation is as follows;
The resulting pdf , with mean zero and variance one, is;
The CDF of the standard normal variable is;
Standard tables are available to get the F(z) values for different z values.