Modeling the outcome of a die

When a fair die is rolled the probability of getting any number between 1 and 6 is 1/6 and it is same for all the numbers. It is also difficult to say what would be the probable outcome when the die is rolled. This uncertainty is very difficult to explain and may be termed as aleatory uncertainty.

Suppose a die is rolled for six times, the probabilities associated to the each outcome may be as follows. As discussed earlier, the probability associated to each outcome in case, if the die is fair, 1/6, but if it is an unfair die the associated probabilities are to be calculated based on the outcomes of the six rolls. If the six outcomes are 1, 2, 2, 3, 4, and 5 the corresponding probabilities may be as given in the following table.

Table 1.1: The variability associated to the outcomes of an unknown die

 

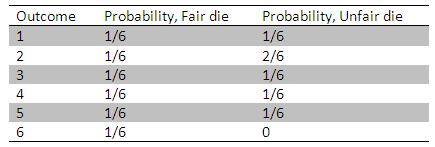
It is possible to get an idea about the kind of die that is being rolled when the experiment is repeated for several times. If the die is fair the probabilities tend to 1/6 and if it is unfair the probability associated to a particular outcome tends to be zero (Table 1.1). This kind of uncertainty may be termed as epistemic uncertainty.

The term ‘randomness' is used for inherent variability and the term ‘uncertainty' is used for lack of complete knowledge. It is not easy to differentiate randomness and uncertainty and it depends on the level of understanding about the process. When the experiments involving some natural elements are repeated under similar conditions the outcomes may or may not be the same. Quantification of these uncertainties and the evaluation of their effects on design and implementation require concepts and methods of probability.