Introduction

Uncertainties about certain pure natural processes as well as man-made experiments that are involving some natural elements necessitate the study of probability and statistics. These uncertainties may result in due to,

• the inherent variability (also known as Aleatory variability),
• lack of complete knowledge (Epistemic uncertainty) about the natural process, and
• the inappropriate model chosen to study the process

Aleatory variability

In many of the civil engineering fields the data are random in nature and contain lot of variability and the reasons for the variability are beyond the comprehension of the civil engineer. This inherent variability is also known as the Aleatory variability. The best example is the rainfall in a particular month of the year and the variability in the magnitude of the rainfall, when observed over several years, is completely random. Similarly, the time gaps between the vehicle arrivals (during off-peak hours) at a particular location of the road are completely random and the gap data between the vehicular arrivals contain lot of variability.

Epistemic Uncertainty

Unlike the Aleatory variability, the epistemic uncertainty results in due to the inability of the modeler to comprehend the system in the form of a mathematical/simulation model.

 

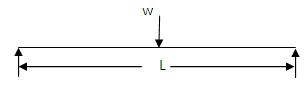
Figure 1.1: Simply supported beam with concentrated load

Deflection of a simply supported beam under a concentrated load, shown in Figure 1.1, can be found easily using the following formula.

Where L is the length of the beam, W is the load applied, E is the young's modulus, and I is the moment of Inertia of the beam section.

But this formula is based on several assumptions like the ones given below;

1. The material is linearly elastic
2. Even after bending the plane section of the beam remains plane
3. Stress strain relationship is same in compression and tension

Due to these assumptions the actual deflection and the deflection value obtained from the above formula are different. When the same experiment is repeated under exactly similar conditions estimated deflections may vary. This variability is resulting due to the assumptions made in deriving the deflection formula.