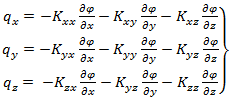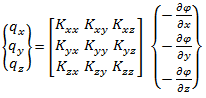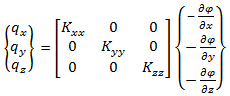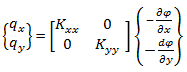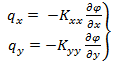In case of anisotropic aquifer, the Darcy’s law can be written as,

(4.12)

This can also be written as

(4.13)

The coefficients appear in equation (4.12) and (4.13) are the component of the second rank tensor of hydraulic conductivity. Since K_xy = K_yx, K_xz = K_zx and K_yz = K_zy there are six distinct components in a three dimensional flow. In case of two-dimensional flow there are only three distinct components to fully define the hydraulic conductivity , i.e.

(4.14)

It may be noted here that the magnitude of the hydraulic conductivity of a porous medium is independent of the coordinate system. However the component K_ij depends on the chosen coordinate system. Further, it is always possible to choose three mutually orthogonal directions in space in such a way that the component K_ij = 0 for i ≠ j and K_ij  ≠ 0 for i = j. These chosen directions in space are called principal directions of an anisotropic medium. As such, when principal directions are chosen, the equation (4.13) becomes

(4.15)

And, in case of 2-dimensional flow

(4.16)

Or,

(4.17)