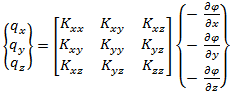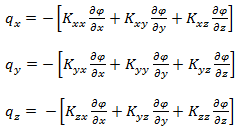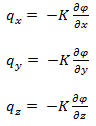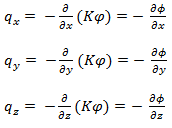The Darcy’s Law was derived experimentally for one dimensional flow in a homogeneous porous medium. The generalized three-dimensional form of the equation can be expressed as,
q = KJ |
(4.1) |
Where,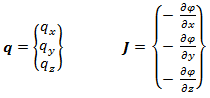 
and 
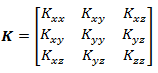
It may be noted that 
where
is any direction. The negative sign also indicates that water is flowing
from higher hydraulic head to lower hydraulic head. Thus hydraulic gradient is negative along the direction of flow.
The equation (4.1) can also be written as
|
(4.2) |
The flow in x, y and z direction can be written as
|
(4.3)
|
In case of flow through homogeneous isotropic medium, the coefficient K is a scalar constant, i.e., the value of K is independent of direction and space. In that case the equation (4.3) to (4.5) become
|
(4.6)
|
It may be noted that the equations (4.6) to (4.8) are also valid for flow through non-homogeneous porous medium as long as the medium is isotropic. In case of flow through homogeneous isotropic medium, the equations (4.6) to (4.8) are also expressed as
|
(4.9)
|
In this case the term Φ = Kφ is called specific discharge potential. It should be noted that the equations (4.9) to (4.11) cannot be used for flow through non-homogeneous and non-isotropic medium.