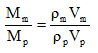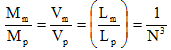5.6 Introduction to geotechnical centrifuge modelling
          A geotechnical centrifuge is used to conduct physical modeling of geotechnical problems for which gravity is the primary driving force. These studies include determination of settlement of embankments, stability of slopes and tunnels, flow and contaminant migration characteristics of soil (Cooke and Mitchell 1991; Singh and Gupta 1999). 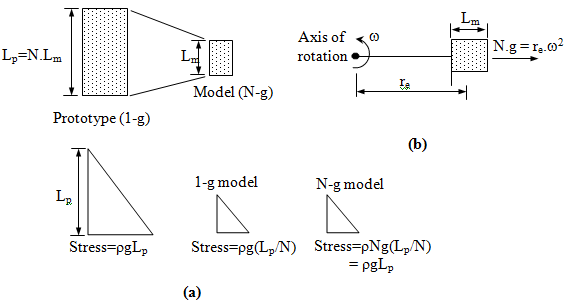The basic principle of centrifuge modelling is that when a soil sample model (N times smaller than its prototype) is subjected to N times the acceleration due to Earth's gravity (Ng) by centrifugation, it results in identical self-weight stresses at homologous points in the model and the prototype as depicted in Fig. 5.9 (a) (Taylor 1995). In the figure, ρ is the mass density of soil, g is the acceleration due to gravity, ω is the angular velocity of rotation in rad/sec, r_e is the effective radius represented by Eq. 5.11, where r_t is the distance from axis of rotation to the top of the soil sample. It can be clearly seen that the stress in prototype and N-g model is identical where as the geostatic stress scale down by N in a 1-g model.

Fig. 5.9 Basic principle of the centrifuge modelling

5.11

5.6.1 Similitude in centrifuge modeling
          The results of centrifuge model, which is used to understand a mechanism or process, can be extrapolated to corresponding prototype condition using suitable scaling laws. To formulate these scaling laws, three types of similitude conditions have to be considered, as discussed in the following.

Geometrical similarity   
This can be achieved if there is a constant ratio of length, L, between the homologous points in the model and the prototype.

5.12

where subscripts m and p correspond to the model and its prototype, respectively, and l is the scale factor.

Kinematic similarity
The model and the prototype are said to be kinematically similar if their ratio of velocity, v, and acceleration, a, are constant. Hence:

vm/vp = β

5.13

am/ap = n

5.14

where β and n are constants.

Dynamic similarity
This similarity can be ensured if there is a constant ratio between the forces in the model and its prototype.

Fm/Fp = x

5.15

where F is the force and x is a constant.

5.6.2 Modeling of mass in Ng model

Mass M = ρ.V

5.16

ρ is the density and V is the volume of soil mass.

5.17

Subscripts m and p stands for model and prototype, respectively.

If the material used in model and prototype are same, then the mass density will be same (ρ_m = ρ_p).

5.18

Unit weight γ = ρ.g

5.19

5.20

For Ng model, ρ_m = ρ_p and g_m = Ng_p

Therefore, γm = Nγp

5.21