|
The base case is given below.
- Cost of travel by car (Equation)=
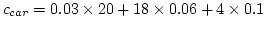 = 2.08 = 2.08
- Cost of travel by bus (Equation)=
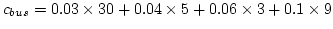 = 2.18 = 2.18
- Probability of choosing mode car (Equation)=
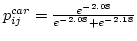 = 0.52 = 0.52
- Probability of choosing mode bus (Equation)=
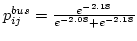 = 0.475 = 0.475
- Proportion of trips by car =
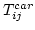 = 5000 = 5000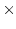 0.52 = 2600 0.52 = 2600
- Proportion of trips by bus =
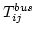 = 5000 = 5000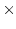 0.475 = 2400 0.475 = 2400
- Fare collected from bus =
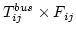 = 2400 = 2400 9 =
21600 9 =
21600
When the fare of bus gets reduced to 6,
- Cost function for bus=
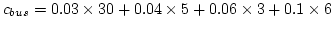 = 1.88 = 1.88
- Probability of choosing mode bus (Equation)=
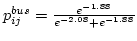 = 0.55 = 0.55
- Proportion of trips by bus =
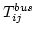 = 5000 = 5000 0.55 = 2750 0.55 = 2750
- Fare collected from the bus
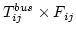 = 2750 = 2750 6 =
16500 6 =
16500
The results are tabulated in table
|