Text_Template

Module 5 : Force Method - Introduction and applications

Lecture 2 : The Force Method

5.3	The Force Method
	The force method is used to calculate the response of statically indeterminate structures to loads and/or imposed deformations. The method is based on transforming a given structure into a statically determinate primary system and calculating the magnitude of statically redundant forces required to restore the geometric boundary conditions of the original structure. The force method (also called the flexibility method or method of consistent deformation ) is used to calculate reactions and internal forces in statically indeterminate structures due to loads and imposed deformations. The basic steps in the force method are as follows:
	(a) Determine the degree of static indeterminacy, n of the structure. (b) Transform the structure into a statically determinate system by releasing a number of static constraints equal to the degree of static indeterminacy, n. This is accomplished by releasing external support conditions or by creating internal hinges. The system thus formed is called the basic determinate structure . (c) For a given released constraint j, introduce an unknown redundant force 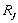corresponding to the type and direction of the released constraint. (d) Apply the given loading or imposed deformation to the basic determinate structure . Use suitable method (given in Chapter 4) to calculate displacements at each of the released constraints in the basic determinate structure . (e) Solve for redundant forces 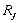( j =1 to n ) by imposing the compatibility conditions of the original structure. These conditions transform the basic determinate structure back to the original structure by finding the combination of redundant forces that make displacement at each of the released constraints equal to zero.
	It can thus be seen that the name force method was given to this method because its primary computational task is to calculate unknown forces , i.e. the redundant forces through .
5.3.1	Selection of the basic determinate structure
	There is no limit to the number of different basic determinate structure that can be generated for a given structure. The choice of structure, however, must ensure that the primary system is stable. In addition, it is recommended that the basic determinate structure be chosen to minimize computational effort and maximize computational accuracy. (a) Stability of Basic determinate structure It is not sufficient merely to release the correct number of statical constraints in generating a basic determinate structure. Care must be taken to ensure that the basic determinate structure is stable. This fact is explained in the Table 5.1 where any arbitrary release of constraint can result into the unstable basic determinate structure.

The force method (also called the flexibility method or method of consistent deformation ) is used to calculate reactions and internal forces in statically indeterminate structures due to loads and imposed deformations.