Example 5.13 Determine the reaction of the propped cantilever beam if the beam is assumed to be subjected to a linear temperature gradient such that the top surface of the beam is at temperature
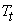 and lower at and lower at 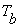 . The beam is uniform having flexural rigidity as EI and depth d . The coefficient of thermal expansion for beam material is . The beam is uniform having flexural rigidity as EI and depth d . The coefficient of thermal expansion for beam material is 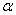 . . |