| |
|
| 5. |
Solution for the unknown displacement |
| |
The algebraic equations obtained in the above step are solved for the unknown displacements. In linear equilibrium equations, this is a straightforward application of matrix algebra techniques. However, for nonlinear problems the desired solutions are obtained by sequence of steps, each step involving the modification of the stiffness matrix and/ or load vector. |
| |
Therefore displacements at nodal points are, 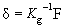 |
| 6. |
Computations of the element stresses and strains at the nodal points |
| |
In some cases the magnitude of the primary unknowns, that is the nodal displacements, will be all that is required for an engineering solution. More often, however, the other quantities derived from the primary unknown like stresses, strains must be computed. |
| |
Force acting on each element is, 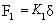 |
| |
|
|