| |
|
| 3. |
Derivation of the element stiffens matrix. |
| |
The stiffness matrix consists of the co-efficient of the equilibrium equations derived from the material and properties of an element and obtained by the use of minimum potential energy. The stiffness relates the displacements at the nodal points (the nodal forces) to the applied forces at the nodal points. The distributed forces applied to the structure are converted into equivalent concentrated forces at nodes. The equilibrium relates the stiffness matrix [K], nodal force vector [F], and the nodal displacement vector [d] is expressed as a set of simultaneous linear algebraic equations. |
| |
Element stiffness matrix, 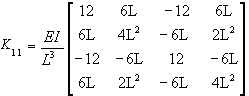 |
| 4. |
Assembling |
| |
This process includes the assemblage of the overall or global stiffness matrix for the entire body from the individual element stiffness matrices and the overall or global forces or load victor from the element nodal vectors. The most common assemblage technique used is called as the direct stiffness matrix [K]. |
| |
[K] {d}=[F] Global stiffness matrix, 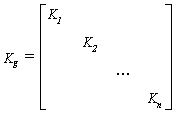 |
| |
|