Module 6 : Traffic Intersection Control

Lecture 32 : Traffic Rotary

1

2

3

4

5

6

7

8

	Numerical example The width of a carriage way approaching an intersection is given as 15 m. The entry and exit width at the rotary is 10 m. The traffic approaching the intersection from the four sides is shown in the figure 1 below. Figure 1: Traffic approaching the rotary 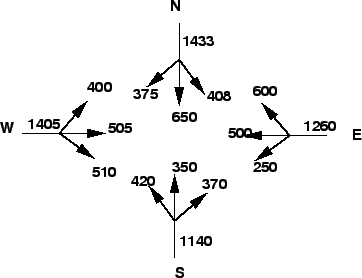Find the capacity of the rotary using the given data. Solution The traffic from the four approaches negotiating through the roundabout is illustrated in figure 2. Figure 2: Traffic negotiating a rotary Weaving width is calculated as, w = $[\frac{e_1+e_2}{2}]+3.5$ = 13.5 m Weaving length, l is calculated as = 4$\times$w = 54 m The proportion of weaving traffic to the non-weaving traffic in all the four approaches is found out first. It is clear from equation,that the highest proportion of weaving traffic to non-weaving traffic will give the minimum capacity. Let the proportion of weaving traffic to the non-weaving traffic in West-North direction be denoted as $p_{WN}$, in North-East direction as $p_{NE}$, in the East-South direction as $p_{ES}$, and finally in the South-West direction as $p_{SW}$. The weaving traffic movements in the East-South direction is shown in figure 3. Then using equation, $p_{ES}$ = $\frac{510+650+500+600}{510+650+500+600+250+375}$= $\frac{2260}{2885}$=0.783 $p_{WN}$ = $\frac{505+510+350+600}{505+510+350+600+400+370}$= $\frac{1965}{2735}$=0.718 $p_{NE}$ = $\frac{650+375+505+370}{650+375+505+370+510+408}$= $\frac{1900}{2818}$=0.674 $p_{SW}$ = $\frac{350+370+500+375}{350+370+500+375+420+600}$= $\frac{1595}{2615}$=0.6099 Thus the proportion of weaving traffic to non-weaving traffic is highest in the East-South direction. Figure 3: Traffic weaving in East-South direction Therefore, the capacity of the rotary will be capacity of this weaving section. From equation, $$Q_{ES}= \frac{280\times 13.5[1+\frac{10}{13.5}][1-\frac{0.783}{3}]}{1+\frac{13.5}{54}} = 2161.164 veh/hr.$$ (1)