| |
| | |
|
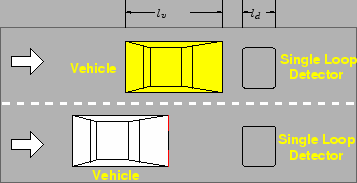
Fig. 1 shows a two-lane unidirectional roadway segment
with single loop detectors installed.Assume that the detection zone length is 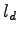 and is equal to the detector
length, the length of the vehicle is and is equal to the detector
length, the length of the vehicle is 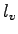 , the speed of the vehicle is , the speed of the vehicle is 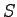 ,
then the actual time (the time period that the vehicle is over the detector) can
be calculated by: ,
then the actual time (the time period that the vehicle is over the detector) can
be calculated by:
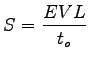 |
(1) |
where,
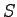 = Spot speed in m/sec = Spot speed in m/sec
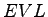 =vehicle length =vehicle length 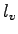 + detector length + detector length 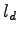
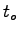 = Occupancy time = Occupancy time
Figure 1:
Layout of a roadway segment with single loop detectors
 |
There are many algorithms for estimating speed by single loop.
The most common method is based on the relationship between fundamental traffic
variables.
It uses a constant or a function to convert loop occupancy into density.
The variables include inductive loop length, average vehicle length, occupancy,
and traffic volume.For the given number of vehicle and duration of the observed data the specimen
speed can find by following Eqn. 2 is shown below.
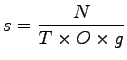 |
(2) |
where,
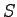 = Space mean speed in m/sec = Space mean speed in m/sec
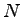 = Number of vehicles in the observed interval = Number of vehicles in the observed interval
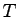 = Observation interval in sec = Observation interval in sec
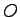 = occupancy time = occupancy time
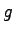 = speed correction factor; (based upon assumed vehicle length, detector
configuration, and traffic conditions) Most of the algorithms followed as (40.9/6.55) for average vehicle length 6.55m. = speed correction factor; (based upon assumed vehicle length, detector
configuration, and traffic conditions) Most of the algorithms followed as (40.9/6.55) for average vehicle length 6.55m.
Example-2
The length of vehicle is 4 m and the length of loop detector zone is 1.83 m.
The time occupancy in the loop is 0.3 sec, find the spot speed of the vehicle?
Solution:
From the given data the average vehicle length is 4 m and the length of loop
detector zone is 1.833 m, the time occupancy in loop is 0.3 sec substitute in
Eqn. ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) . .
Example-3
In freeway 2500 vehicles are observed during 300 sec interval.
The loop occupancy is 75 percentages and the average length of vehicle observed
as 6.55 m, find the space mean speed on the freeway section?
Solution
Given data is number of vehicle is 2500, duration is 300 sec, loop occupancy is
75 percentage, the average length of vehicle is 6.55 so speed correction factor
is 40.99/6.55 substitute in Eqn. 2.
|
|
| | |
|
|
|