| |
| | |
|
Dual-loop detectors are also called speed traps, T loops, or double loop
detectors.
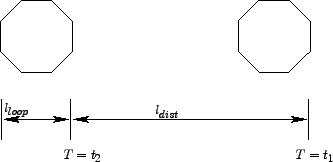
In a dual-loop system, two consecutive single inductance loops, called ``M
loop'' and ``S loop'', are embedded a few distance apart as shown in
Fig. 1.
With such a design, when one of them detects a vehicle, timer is automatically
started in the dual-loop system and runs until the same vehicle is detected by
other loop.Thus, in addition to outputs of vehicle count and occupancy data, individual
vehicle speeds can be trapped through the dividend of the distance between those
two single loops 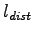 by the elapsed time.
Speed trap is defined as the measurement of the time that a vehicle requires to
travel between two detection points.
Spot speed is measured by following Eqn. 1. by the elapsed time.
Speed trap is defined as the measurement of the time that a vehicle requires to
travel between two detection points.
Spot speed is measured by following Eqn. 1.
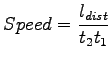 |
(1) |
where,
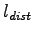 = Distance between two loops in meters = Distance between two loops in meters
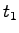 = Vehicle entry time at first loop in sec = Vehicle entry time at first loop in sec
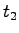 = Vehicle entry time at second loop in sec = Vehicle entry time at second loop in sec
Dual-loop detectors can also be used to measure vehicle lengths with extra data
extracted from controllers’ records.
The length of vehicle is measured by following Eqn. 2:
 |
(2) |
where,
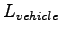 = Length of vehicle in meters. = Length of vehicle in meters.
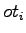 = on-time for loop detector i; Speed in m/sec = on-time for loop detector i; Speed in m/sec
Figure 1:
Schematic diagram of dual loop detectors
 |
Example-1
If the vehicle entering the freeway in loop M at time 8:32:22:00 am and leaving
loop N at time 8:32:22:15 am, the distance between two loops will be 3.66 m.
Find the spot speed of the vehicle.
Also find the length of the vehicle if time occupancy for M - loop is 0.25sec
and 0.29 for N - loop.
Solution:
Step 1 Spot Speed calculated from the equation 1, where given that the
distance between two loops are 3.66m and entry, exit times are 8:32:22:00 and
8:32:22:15 substitute in Eqn. 1.
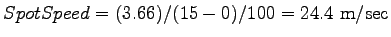 . .
Step 2 The vehicle length can obtained by the spot speed of the
vehicle, so substitute the occupancy times at exit and entry in the
Eqn. 2.
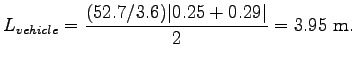 |
(3) |
|
|
| | |
|
|
|