Elasticity of a crosslinked network
We have so far deduced the extensional force required to stretch a single chain by a distance x. Now, we will consider not a single chain but a network of chains in which the chains are permanently connected in certain randomly distributed joints. This kind of network occurs for rubber like materials in which the crosslinkages are introduced by vulcanization of the rubber. When the rubber material is deformed by applying some external stress, it alters the positions of these crosslinkages and thus internal state of the network. The states of the network can be represented by a system of vectors connecting neighboring crosslinking points. Let us mark the volume elements surrounding each crosslinking point as 1, 2, 3 … Then the number of vectors terminating each volume element can be represented by vi so that the total number v of chains remain constant 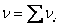 . Each such chain can assume number of configurations by altering the intervening portion while its end-to-end displacement vector remain unaltered. The relative number of such configurations for a chain having vector terminating to i-th cell with co-ordinates . Each such chain can assume number of configurations by altering the intervening portion while its end-to-end displacement vector remain unaltered. The relative number of such configurations for a chain having vector terminating to i-th cell with co-ordinates 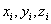 are are 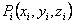 . Hence this quantity for vi number of such chains is . Hence this quantity for vi number of such chains is 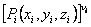 . Then the probability for the entire network to be found at a particular configuration is obtained by finding the product of all such probability over all the volume elements, . Then the probability for the entire network to be found at a particular configuration is obtained by finding the product of all such probability over all the volume elements,
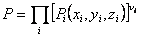 |
(36.9) |
The entropy of the network is then found as
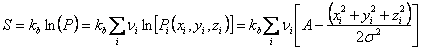 |
(36.10) |
Since the cross-linkages are introduced in random manner in the undeformed state of the network, the number of chains vi terminating in the i-th volume element can be written as,
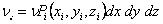 |
(36.11) |
|