Highly stretched chain

The Gaussian probability distribution is a good description of chain behavior at small displacements from equilibrium. It shows that the force required to produce an extension x in the end-to-end distance is

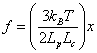(36.4)

which can be written as,

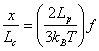(36.5)

                       
However if the segments of the chain are individually inextensible, the force required to extend the chain should diverge as the chain approaches its maximum extension, 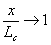. Such a divergence is not predicted by equation 36.4, signifying that the Gaussian distribution becomes increasingly inaccurate and finally invalid as the chain is stretch to its contour length. The force-extension for rigid freely jointed rods can be obtained analytically. This solution has the form,

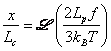(36.6)

where 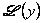is the Langevin function given as,

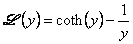(36.7)

Note that x is the projection of the end-to-end displacement in the direction of the applied force. For small values of f, equation 36.6 reduces to Gaussian expression in equation 14.59. For very large value of f the Langevin function tends to 1, so that x asymptotically approaches .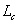

Although, the force-extension data derived from the freely jointed rod model gives reasonably accurate data for bio-polymers, its main drawback lies in the assumption of the chain segments being rigid. Actually, for bio-polymers like microtubules, DNA, the filaments are continuously flexible, so that they are better described by the worm-like-chain (WLC) model. The following relation describes a nearly accurate description of the WLC model which has been very useful in describing the extension of DNA,

(36.8)