Entropic elasticity
As mentioned earlier, far more chain configurations have end-to-end displacement close to the mean value of 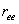 than to the chain contour length than to the chain contour length 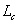 . From statistical thermodynamics, it can be shown that entropy is proportional to the logarithm of the number of configurations: . From statistical thermodynamics, it can be shown that entropy is proportional to the logarithm of the number of configurations:
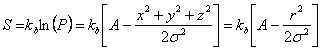 |
(36.1) |
so that maximum entropy occurs for 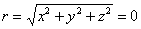 and it decreases as the chain is stretched from its equilibrium length. For free joined chains, the configurations all have vanishing energy, so that the Helmhotz free energy of a chain is defined as, and it decreases as the chain is stretched from its equilibrium length. For free joined chains, the configurations all have vanishing energy, so that the Helmhotz free energy of a chain is defined as, 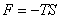 . Thus with increase in F, e.g. the chain is stretched, S decreases, i.e. work must be done to stretch the chain and it is elastic by virtue of its entropy. The force of retraction arising from the entropy change is . Thus with increase in F, e.g. the chain is stretched, S decreases, i.e. work must be done to stretch the chain and it is elastic by virtue of its entropy. The force of retraction arising from the entropy change is
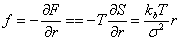 |
(36.2) |
Thus the effective spring constant of the chain is be found out 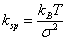 where, where, 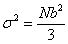 for a three dimensionally oriented chain. Thus the expression for spring constant is obtained as, for a three dimensionally oriented chain. Thus the expression for spring constant is obtained as,
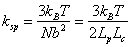 |
(36.3) |
It should be noted that 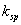 increases with temperature which can be readily verified in experiments. increases with temperature which can be readily verified in experiments.
|