Elasticity of a crosslinked network

Now say the network is elongated in the z direction by a factor . Then assuming that the relative positions of the network junctions change according to the macroscopic dimension of the sample, the z co-ordinate of each joint alters by a factor  and the x and  y co-ordinates alter by . Thus the volume remains constant. To say it somewhat differently a junction which possess a new position z after stretching, actually was in  before stretching and its x and  y co-ordinates were  and  . Using these new co-ordinates, the expression for the probability  from equation 35.16 can be written as

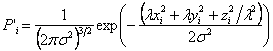(36.12)

Then from equations 36.10 and 36.11, replacing the summation sign by integral sign, the expression for entropy is obtained as.

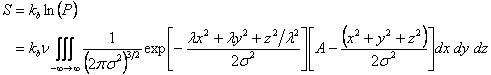(36.13)

The above integral has been estimated for change of entropy because of passing from undeformed to deformed state:

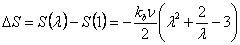(36.14)

Then entropic contribution to the elastic force can be obtained as,

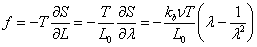(36.15)

Where L₀ is the initial length of the sample. Thus we obtain a new law relating force of extension and the extent of extension.