Random chain in one dimension:
Consider a one-dimensional chain with three segments, each chain starting off the origin and a link in the chain can point to the left or to the right. Since each link has two possibilities, there are 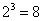 configurations possible for the whole chain. Representing configurations possible for the whole chain. Representing 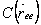 as the number of configurations with a particular displacement as the number of configurations with a particular displacement 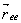 , the eight configurations are distributed as , the eight configurations are distributed as
It is easy to see that these quantities are the binomial coefficients of 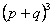 . For a chain with Nsegments, with i vectors pointing left and N-i vectors pointing right, the number of such configurations are same as the coefficient of the binomial expansion of . For a chain with Nsegments, with i vectors pointing left and N-i vectors pointing right, the number of such configurations are same as the coefficient of the binomial expansion of
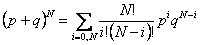 |
(35.6) |
i.e.  . This chain with N segments can be thought of to be a random walk with each segment having probability . This chain with N segments can be thought of to be a random walk with each segment having probability 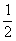 of pointing to the left and probability of pointing to the left and probability 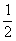 of pointing to the right. Hence the probability for there to be a configuration with i segments pointing left and N-i segments pointing right is of pointing to the right. Hence the probability for there to be a configuration with i segments pointing left and N-i segments pointing right is
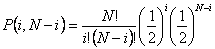 |
(35.7) |
The probability is appropriately normalized, so that the summation of all the probabilities yield 1,
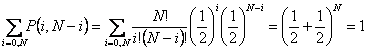 |
(35.8) |
As the number of links in the chain increases, the distribution looks more and more continuous, eventually the distribution converges to that of the Gaussian distribution, which is of the form,
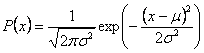 |
(35.9) |
This expression is the probability density such that the probability of finding a state between x and x+dx is P(x)dx. The mean value 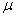 of the distribution can be found out as, of the distribution can be found out as,
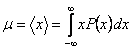 |
(35.10) |
And its variance as,
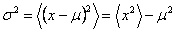 |
(35.11) |
For one Cartesian component of 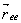 in a random chain, in a random chain, 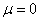 , because the vectors , because the vectors 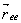 are isotropically distributed; furthermore, are isotropically distributed; furthermore, 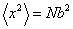 , which implies , which implies 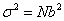 in one dimension. in one dimension.
|