Random chain in three dimensions:
The configuration of a chain in three diemension can be projected onto three axes of the Cartesian system and then can be treated as three independent one dimensional systems. Thus x component of the end-to-end distance is the summation of the individual vectors as projected on the x axis:
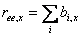 |
(35.12) |
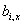 is the x-projection of monomer vector is the x-projection of monomer vector 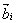 . For freely jointed chain, . For freely jointed chain, 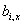 is independent of is independent of 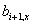 , so the projections form a random walk in one dimension, although of variable lengths, even if all the monomenrs are of the same length. If the number of segments is large the probability distribution with variable segment lengths has the same form as that of with uniform segment length: , so the projections form a random walk in one dimension, although of variable lengths, even if all the monomenrs are of the same length. If the number of segments is large the probability distribution with variable segment lengths has the same form as that of with uniform segment length:
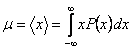 |
(35.13) |
with a variance 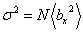 . Here . Here 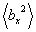 is the expectation of the projection of individual segments on the x axis. The system is however symmetric, which should ensure that the mean projections are independent of direction, so that, is the expectation of the projection of individual segments on the x axis. The system is however symmetric, which should ensure that the mean projections are independent of direction, so that,
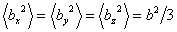 |
(35.14) |
because, 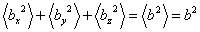 for segments of constant length. Hence the variance is, for segments of constant length. Hence the variance is,
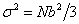 |
(35.15) |
Now the probability of finding a three dimensional chain within the volume 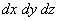 centered on the position centered on the position 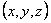 is is 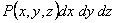 , c is the product of the probability distributions in each of the Cartesians directions, , c is the product of the probability distributions in each of the Cartesians directions,
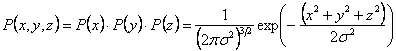 |
(35.16) |
in which 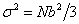 and and 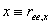 etc. According to equation 14.49, the most probable co-ordinate for the tip of the chain is etc. According to equation 14.49, the most probable co-ordinate for the tip of the chain is 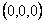 , that does not mean that the most likely value of , that does not mean that the most likely value of 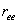 is zero. In fact the most likely value of is zero. In fact the most likely value of 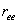 can be estimated by considering that the probability for the chain to have radial end to end distance between r and r+dr is, can be estimated by considering that the probability for the chain to have radial end to end distance between r and r+dr is, 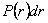 . Here . Here 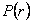 is the probability per unit length, defined as: is the probability per unit length, defined as: 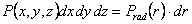
so that,
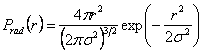 |
(35.17) |
Deriving 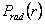 with respect to r and equating it to zero, one obtains the most likely value of r, with respect to r and equating it to zero, one obtains the most likely value of r,
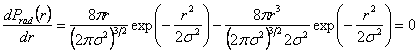 |
(35.18) |
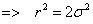 |
Substituting the expression for 35.15 in 35.18, one obtains the expression,
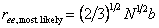 |
(35.19) |
The average value of 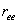 is obtained as, is obtained as,
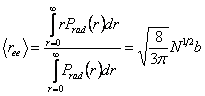 |
(35.20) |
And the mean square end to end distance is obtained as,
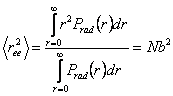 |
(35.21) |
|