Let’s say we are concerned with the special case in which all segments of the chain has the same length 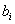 although their orientations differ. For a random chain, bond vector although their orientations differ. For a random chain, bond vector 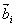 can assume any orientation independent of can assume any orientation independent of 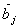 , so that the result , so that the result 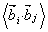 vanishes. In other word only the diagonal terms remain which equals vanishes. In other word only the diagonal terms remain which equals 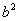 . Then a chain with random orientation obeys, . Then a chain with random orientation obeys,
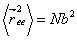 |
(35.4) |
Furthermore using 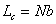 , we obtain , we obtain
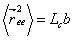 |
(35.5) |
which is similar to equation 14.35 for 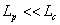 , with , with 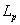 being replaced by being replaced by 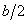 . .
Chain configurations and elasticity:
The tangent correlation function or the end-to-end distance does not really give the complete picture of the configuration of the chain, the probability distribution of its end-to-end distance. These distributions confirm that it is highly unlikely that a random chain will remain in a fully stretched condition, because the most likely value of 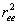 for a freely jointed chain is not far from the value of for a freely jointed chain is not far from the value of 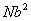 . Basically there are far more configurations available for . Basically there are far more configurations available for 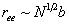 than available for than available for 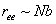 . Because of this when an external load is applied to straighten a chain its entropy decreases, i.e. the chain behaves elastically because of its entropy. . Because of this when an external load is applied to straighten a chain its entropy decreases, i.e. the chain behaves elastically because of its entropy.
|