The equation simplifies in two limits. If 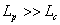 , equation (34.13) is simplified by writing , equation (34.13) is simplified by writing 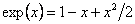 reduces to reduces to 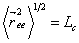 . The filament rather appears like a rod with end-to-end distance close to the contour length. At the other extreme, . The filament rather appears like a rod with end-to-end distance close to the contour length. At the other extreme, 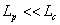 , equation 14.34 simplifies to , equation 14.34 simplifies to
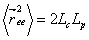 |
(35.1) |
implying that over long distance compared to persistence length 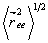 grows like the square root of the contour length, rather than the contour length itself. grows like the square root of the contour length, rather than the contour length itself.
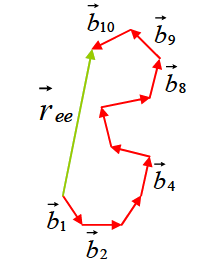
We can now repeat this calculation by discrete representation to relate the geometry of a continuous polymer to its monomeric constituents. The filament is replaced by N segments, each of which is described by a vector 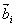 having the same length and orientation as the segment. The end-to-end distance having the same length and orientation as the segment. The end-to-end distance 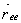 is then represented as is then represented as
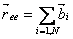 |
(35.2) |
Taking the ensemble average of all chains with the same number of links N, the mean squared end to end displacement is
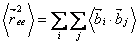 |
(35.3) |
|