Surface instability of a homogeneous half-space
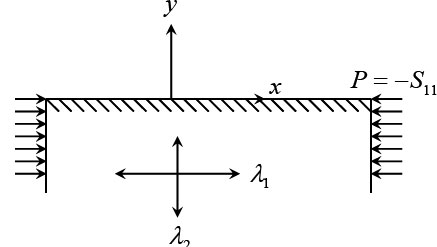
Figure 29.2
Consider a rubber block, an elastic half space, is subjected to a state of initial stress such that it is under compression in 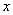 direction but under zero stress along the direction but under zero stress along the 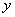 direction: direction:
Since the material is incompressible, the extension ratios satisfy the following relation:
Here 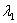 and and 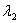 are extension ratios along are extension ratios along 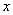 and and 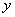 directions respectively. And directions respectively. And 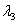 is the extension ratio along the direction normal to the is the extension ratio along the direction normal to the 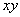 plane. Then the stress-strain relations in equation 29.7 yield: plane. Then the stress-strain relations in equation 29.7 yield:
Where, 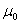 is the shear modulus of the rubber block in unstressed state. Under this initial stress condition the block undergoes incremental deformation in the is the shear modulus of the rubber block in unstressed state. Under this initial stress condition the block undergoes incremental deformation in the 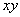 plane. Then the incremental stresses and strain can be represented by equations 29.10 . In addition, we have the incompressibility condition: plane. Then the incremental stresses and strain can be represented by equations 29.10 . In addition, we have the incompressibility condition:
The equilibrium relations for incremental stresses can be written as,
Notice that equation 29.14 can be satisfied by putting the following substitutions:
Where 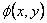 is a stress function which is deduced by solving the stress equilibrium relations subjected to relevant boundary conditions. We can write the stress components is a stress function which is deduced by solving the stress equilibrium relations subjected to relevant boundary conditions. We can write the stress components 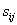 in equation 29.10 in terms of that presented in 29.15, which yield, in equation 29.10 in terms of that presented in 29.15, which yield,
|