Further eliminating the mean incremental stress 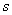 in equation 29.16, we obtain the following equation in terms of in equation 29.16, we obtain the following equation in terms of
After algebraic manipulation of equation 29.18, we obtain
Notice that the perturbation solutions can be considered sinusoidal along the 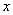 direction which vanishes at infinite depth direction which vanishes at infinite depth 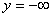 . Such a solution can be represented by the following functional forms: . Such a solution can be represented by the following functional forms:
In which, 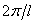 defines the wavelength of the instability. The other parameters can be related as defines the wavelength of the instability. The other parameters can be related as
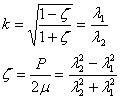 |
(29.21) |
Since, 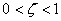 , , 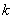 is real and satisfies the inequality is real and satisfies the inequality 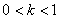 . .
We will now consider the boundary conditions at the surface of the block, which from equation 28.1(b) can be written as
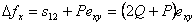 |
|
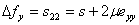 |
(29.22) |
The condition that no incremental force is applied at the surface demands that at 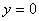 , ,
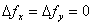 |
(29.23) |
Substituting the solutions  and and 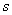 in equation 29.22 and eliminating for constants we obtain the characteristic equation, in equation 29.22 and eliminating for constants we obtain the characteristic equation,
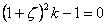 |
(29.24) |
Substituting the expression for 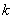 from 29.21 into 29.24 yields from 29.21 into 29.24 yields
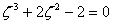 |
(29.25) |
Which has one real root, 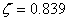 at which the surface turns unstable. From equation 29.21 , the value of at which the surface turns unstable. From equation 29.21 , the value of 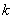 at which instability occurs is obtained as at which instability occurs is obtained as 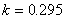 . Notice that the characteristic equation is independent of . Notice that the characteristic equation is independent of 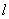 , which implies that surface can become unstable for all wavelengths. , which implies that surface can become unstable for all wavelengths.
We can further calculate the initial extension ratios at which the surface becomes unstable, by putting the following,
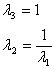 |
(29.26) |
Which yields the extension ratio corresponding to instability as 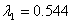 and the compressive stress as and the compressive stress as 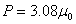 . .
|