Hookean Elastic Material

Let us now consider a Hookean rubbery elastic material, for which the strain energy density function can be written as,

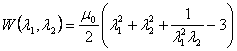(29.6)

Then the initial stress relations as in 28.11 are obtained as,

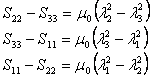(29.7)

Similarly the relations for incremental stresses are obtained as,

(29.8a)

Hence,

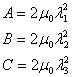(29.8b)

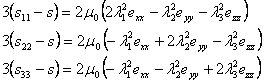(29.8c)

Finally we can derive the elastic constants,

(29.8d)

If the incremental stresses are applied in plane strain, the equations 29.8 get modified to the following:                                         

(29.9)

Which finally results in                                             

(29.10)