The slide modulus
Let us consider a rectangle block which is subjected to initial stresses 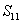 and and 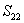 along two principal directions 1 and 2 respectively. along two principal directions 1 and 2 respectively.
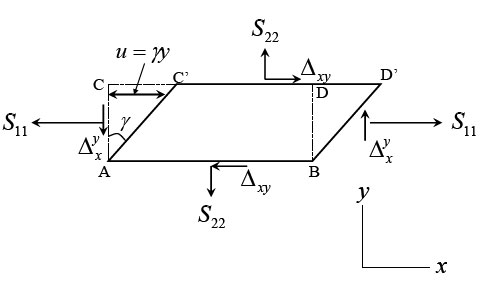
Figure 29.1
Over and above these initial stresses, let us say that it is subjected to shear displacement parallel to the 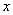 direction. Then the displacement components are, direction. Then the displacement components are,
This is an in plane deformation in the 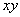 plane. The rectangle ABDC in this plane is deformed into the parallelogram ABD’C’. In order to produce this deformation, we have applied a tangential force on the CD which can be evaluated from the relation of boundary condition as in equations 13.17; substituting plane. The rectangle ABDC in this plane is deformed into the parallelogram ABD’C’. In order to produce this deformation, we have applied a tangential force on the CD which can be evaluated from the relation of boundary condition as in equations 13.17; substituting 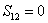 , we obtain , we obtain
These expressions represent the incremental forces acting on a face of the material when the normal directions are defined by the direction cosines, 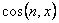 and and 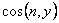 . For the shear displacement we may write, . For the shear displacement we may write,
From the stress-strain relations of 13.39 and 13.40 we may derive,
Hence the expression in 29.2 yields,
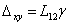 represents the tangential stress applied to the face CD in order to produce the tangential stress represents the tangential stress applied to the face CD in order to produce the tangential stress 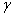 in which the quantity in which the quantity 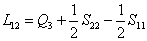 is called the measurable slide modulus. is called the measurable slide modulus. 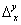 represents the vertical stress which is applied to the sides AC and BD. This analysis may be repeated for other co-ordinate planes. represents the vertical stress which is applied to the sides AC and BD. This analysis may be repeated for other co-ordinate planes.
|