An estimation of 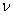 can be obtained by considering the geometry of the packing. For example, we can assume that the particles are closed pack in hexagonal lattice, so that they interact via an attractive central force and a repulsive steric interaction. Consider a single rhombic cell in the lattice as shown in Figure 21.2. In the undeformed state, its width and height are can be obtained by considering the geometry of the packing. For example, we can assume that the particles are closed pack in hexagonal lattice, so that they interact via an attractive central force and a repulsive steric interaction. Consider a single rhombic cell in the lattice as shown in Figure 21.2. In the undeformed state, its width and height are 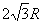 and and 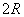 respectively where respectively where 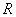 is the particle radius. Let us say that the two central particles are displaced by a distance is the particle radius. Let us say that the two central particles are displaced by a distance 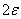 , so that the width of the rhombus decreases to , so that the width of the rhombus decreases to 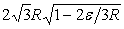 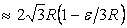 . Hence the strain can be defined as . Hence the strain can be defined as 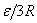 . At the same time, the height of the rhombus increases to . At the same time, the height of the rhombus increases to 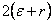 , so that the strain developed is , so that the strain developed is 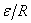 . So that the Poisson ratio defined as the ratio of two strains is deduced as . So that the Poisson ratio defined as the ratio of two strains is deduced as 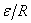 . .
Analysis of the geometry yields also the numerical estimate of the Young's modulus of the layer. For close hexagonal packing of spherical particles, the area fraction of the particles can be deduced as, 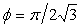 , which gives a typical value of the Young's modulus as, , which gives a typical value of the Young's modulus as,
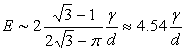 |
(21.6) |
In actual practical situations however the particles are expected to be irregular without any ordered packing which will yield some other value of the pre-factor. Nevertheless, the expression in equation 21.6 shows that the elastic property of the layer depends on the surface tension of the liquid and the diameter of the particles. The above expressions for the elastic modulus can be verified by another experiment which involves first sprinkling on the air-water interface hydrophobic particles and then subject the two dimensional particle raft to sufficient compression. This results in elastic buckling as shown in figure 21.1, the wavelength of which can be measured by using a camera. Such measurements can be done by spreading hydrophobic particles of different particle sizes. We can then infer from this data, the value of the Young's modulus.
|