We use the classical theory of elasticity in order to determine the effective mechanical properties of the two dimensional solid from the measurement of the wavelength. We assume the raft to be a thin, isotropic, homogeneous elastic sheet of thickness equal to the particle diameter d . Since, the wavelength is large compared to the particle size, the plane stress conditions apply. We further assume that at the onset of the buckling instability, the deflection of the raft and its vertical displacement 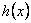measured from its equilibrium position is small. Then, balance of forces yield the following equilibrium equation for plate,

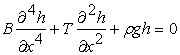(21.7

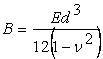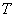in which is the bending stiffness of the plate, is the compressive force per unit length of the plate, 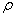is the specific gravity of the liquid and is the acceleration due to gravity. The above equation depicts the summation of three different of forces: the bending force of the plate occurring because of its buckling and the weight of the liquid column of height 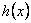, both these force provide stability to the plate; the third component is the compressive force which drives the instability. Substituting 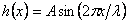into equation 21.7 we obtain,

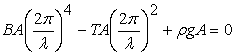(21.8)

Rearranging equation 21.8, we obtain an expression for the compressive load 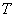as a function of the wavelength

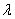
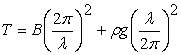(21.9)

We then find an expression for 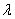at which minimum compressive load needs to be exerted on the layer for the onset of the instability, by putting :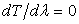

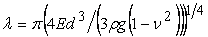(21.10)

Rearrangement of above equation yields an expression for the Young's modulus of the layer as

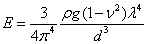(21.11)