| |
For a conventional two-dimensional elastic solid, the mean stress can be written as, 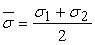 and the mean strain as, and the mean strain as, 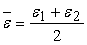 . The stress can be related to strain as, . The stress can be related to strain as,
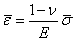 |
(21.1) |
Where 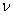 is the Poisson ratio of the solid. We can replace the stress by an isotropic tension averaged over the thickness of the layer, is the Poisson ratio of the solid. We can replace the stress by an isotropic tension averaged over the thickness of the layer, 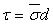 , which then yields, , which then yields,
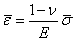 |
(21.2) |
We can then consider that because of infinitesimal change in the tension, the strain changes infinitesimally, so that,
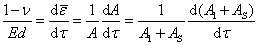 |
(21.3) |
Where, 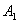 and and 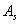 are the area covered by liquid and solid particles respectively and are the area covered by liquid and solid particles respectively and 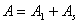 is the total area of the system. Now, the solid particles are rigid at the individual level so that, regardless of the tension applied, the area covered by them is constant, however, the raft as a whole can be soft, because it also consists of the liquid. Equation 21.3 then simplifies to is the total area of the system. Now, the solid particles are rigid at the individual level so that, regardless of the tension applied, the area covered by them is constant, however, the raft as a whole can be soft, because it also consists of the liquid. Equation 21.3 then simplifies to
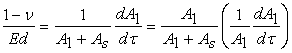 |
(21.4) |
Notice, that the quantity in the bracket is a measure of the surface tension of the liquid, so that 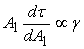 , Equation 21.4, can then be rearranged to yield an expression for the effective Young's modulus of the monolayer , Equation 21.4, can then be rearranged to yield an expression for the effective Young's modulus of the monolayer
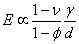 |
(21.5) |
Where 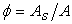 is the area fraction occupied by the solid particles at the interface. Notice that the above expression for is the area fraction occupied by the solid particles at the interface. Notice that the above expression for 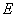 has the property that as has the property that as 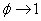 , , 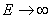 , which is consistent with the fact that the monolayer consists of particles which are rigid. , which is consistent with the fact that the monolayer consists of particles which are rigid.
|