Transformation of stress components (contd...)
Let's now consider transition of stress components from one coordinate system 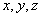 to a new coordinate system to a new coordinate system 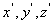 . Let the direction cosines of the new system w.r.t the old one is . Let the direction cosines of the new system w.r.t the old one is
Let's say, 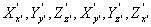 represent the stress components in the new system, while, represent the stress components in the new system, while, 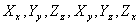 represent those in the old system. Then following previous discussions, represent those in the old system. Then following previous discussions,
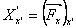 , so that , so that 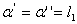 , , 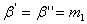 and and 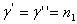
Then from 2.17,
Similarly, we obtain other equations,
If we add the three equations 2.18a and use the following relations,
we obtain the following:
That is, the expression 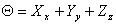 is invariant with respect to transformation of coordinates, i.e. the sum of normal stress components acting on three mutually perpendicular planes do not depend upon the orientation of the planes. is invariant with respect to transformation of coordinates, i.e. the sum of normal stress components acting on three mutually perpendicular planes do not depend upon the orientation of the planes.
Consider again 2.17, if 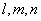 are the direction cosines of the normal are the direction cosines of the normal 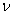 , then the equation yields following expression for the normal stress, , then the equation yields following expression for the normal stress,
Now consider a vector 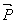 which is of length which is of length 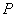 and has end points as the origin of the coordinate system and the point and has end points as the origin of the coordinate system and the point 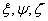 ; then using, ; then using,
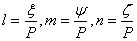
equation 2.20 yields,
in which 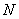 has a physical meaning, so can not depend on the particular choice of axes and the quantity has a physical meaning, so can not depend on the particular choice of axes and the quantity 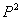 does not depend on the choice of coordinates. Consequently, the quadratic does not depend on the choice of coordinates. Consequently, the quadratic 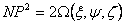 is an invariant of transformation of coordinates. Then, let us put is an invariant of transformation of coordinates. Then, let us put 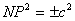 , where , where 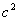 is an arbitrary constant and it has the dimension of a force. It has the same direction as that of is an arbitrary constant and it has the dimension of a force. It has the same direction as that of 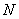 i.e. for a tensile stress it is positive and for a compressive stress it is negative. i.e. for a tensile stress it is positive and for a compressive stress it is negative.
|