Transformation of stress components (contd...)
Let one end of the vector 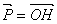 be at the origin O of the coordinate system, then the other end be at the origin O of the coordinate system, then the other end 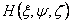 of the vector of the vector 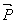 will lie on the surface will lie on the surface 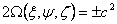 , i.e. , i.e.
Surface 2.22 is a quadratic with the center at the origin; it is called a stress surface.
A direction with the property that only a normal stress acts on the plane normal to it is called a principal direction of stress or a principal axis of stress. Corresponding stress is called the principal stress.
If I select the coordinate axes along the three principal axes of stress, then its equation is known to have the form:
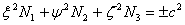
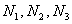 are the values of the quantities are the values of the quantities 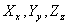 for the new coordinate axes. These values are obtained by solving the following equation: for the new coordinate axes. These values are obtained by solving the following equation:
where 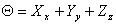 , , 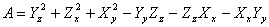
and B = 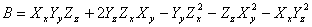
Since 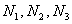 do not depend on the choice of the coordinate system, the coefficients do not depend on the choice of the coordinate system, the coefficients 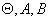 do not depend on it, i.e. these quantities are invariant w.r.t. the transformation of orthogonal rectilinear system of axes. do not depend on it, i.e. these quantities are invariant w.r.t. the transformation of orthogonal rectilinear system of axes.
If the quadric in equation 2.23 are referred to as principal axes, then the tangential tractions across the coordinate planes become zero. There are three such systems of orthogonal planes which are called principal plane of stress and the normal tractions are called the principal stresses. Hence in order to completely specify the stresses at any point in a body we need to know the principle stresses and their directions.
|