Transformation of stress components:
Actually above discussions can be generalized in the form of following proposition.
Let there be two planes passing through the one and the same point: the projection of stress, acting on the first plane on the normal to the second plane is equal to the projection of stress, acting on the second plane on the normal to the first plane .
It should be possible to express the components of the stress at any point with respect to a given system of axes in terms of those referred to another orthogonal system of axes.
Let 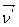 be the normal to plane 1. Its direction cosines are be the normal to plane 1. Its direction cosines are 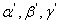 . Then . Then 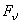 be the stress vector acting on plane 1, its components are, be the stress vector acting on plane 1, its components are,
Let 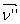 be the normal to plane 2. Its direction cosines are be the normal to plane 2. Its direction cosines are 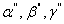 . Then the projections of components of . Then the projections of components of 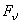 on normal on normal 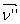 are: are:
The above expression is quite symmetric with respect to 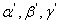 and and 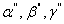 so that the two planes can be interchanged without altering the expression, but that proves the proposition. so that the two planes can be interchanged without altering the expression, but that proves the proposition.
|